BART’s tree structure implementation
Published:
As we commented in the previous post, BART is a sum-of-trees model where each tree is a decision tree. Thus, to implement the BART model first we have to implement the tree structure used by it. The tree implementation will need:
- A data structure to link the nodes. This should allow us to randomly access a node in the tree and to easily add and delete a node.
- Two types of nodes that make up the tree: splitting nodes and leaf nodes. The splitting nodes will be responsible for the division of the predictor space and gather the logic to traverse tree given an element $x$; the leaf nodes have the responses $\mu_{ij}$ for the tree.
- Functions to grow and prune the tree.
- Checks of correctness of the tree.
Data structure to link the nodes
Two types of data structures were consider:
- A series of linked nodes were each node has a link to its left and right children nodes, if they exist. The root node represents the whole tree, since you can traverse the whole tree from it.
- A dictionary that represents the nodes stored in breadth-first order, based in the array method for storing binary trees.
We started coding the linked nodes structure, inspired by this implementation of a binary tree. This structure made creation and deletion of nodes easy since we only needed to replace links to nodes. But, early on, we realized that this implementation would not allow us to randomly access a node in the tree. Thus, we dropped it only maintaining code to represent the tree as a string.
Therefore, we thought of a structure that would explicitly represent the nodes and its positions. Assume we have a complete binary tree, binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. If we walk through the tree in a breadth-first order and number the nodes from zero to number of nodes minus one we can identify every node and its position in the tree structure by this number.
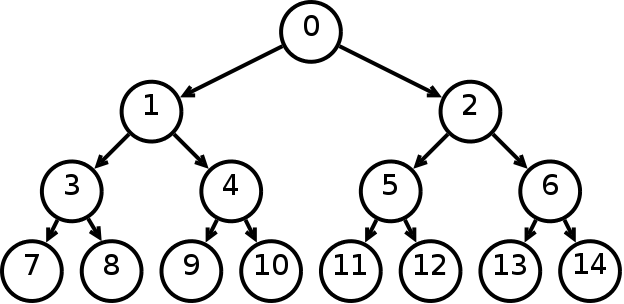
A complete binary tree is efficiently implemented as an array, where a node at location $i$ has children at indexes $2i + 1$ and $2i + 2$ and a parent at location $\left \lfloor{(i - 1) / 2}\right \rfloor $. Since Python doesn’t have a built-in array structure, we consider two basic structures: list and dict.
Note that, although we consider that the indices are taken from numbering a complete binary tree, BART does not necessary construct this type of trees. The only thing we can ensure about the tree structure is that each node of the tree has exactly zero or two children. Yet, this numbering will prove us useful for indexing our structure.
If we try to implement this structure using a list, we would end up with a lot of wasted space since we would have to create dummy nodes to represent non-existent nodes. Thus, we ended up coding the tree structure as a dictionary, where the keys represent the nodes position and the values represent the nodes itself.
class Tree:
def __init__(self):
self.tree_structure = {}
self.num_nodes = 0
self.idx_leaf_nodes = []
def get_node(self, index):
if not isinstance(index, int) or index < 0:
raise TreeStructureError('Node index must be a non-negative int')
if index not in self.tree_structure:
raise TreeStructureError('Node missing at index {}'.format(index))
return self.tree_structure[index]
def set_node(self, index, node):
if not isinstance(index, int) or index < 0:
raise TreeStructureError('Node index must be a non-negative int')
if not isinstance(node, SplitNode) and not isinstance(node, LeafNode):
raise TreeStructureError('Node class must be SplitNode or LeafNode')
if index in self.tree_structure:
raise TreeStructureError('Node index already exist in tree')
if self.num_nodes == 0 and index != 0:
raise TreeStructureError('Root node must have index zero')
parent_index = node.get_idx_parent_node()
if self.num_nodes != 0 and parent_index not in self.tree_structure:
raise TreeStructureError('Invalid index, node must have a parent node')
if self.num_nodes != 0 and not isinstance(self.get_node(parent_index), SplitNode):
raise TreeStructureError('Parent node must be of class SplitNode')
if index != node.index:
raise TreeStructureError('Node must have same index as tree index')
self.tree_structure[index] = node
self.num_nodes += 1
if isinstance(node, LeafNode):
self.idx_leaf_nodes.append(index)
def delete_node(self, index):
if not isinstance(index, int) or index < 0:
raise TreeStructureError('Node index must be a non-negative int')
if index not in self.tree_structure:
raise TreeStructureError('Node missing at index {}'.format(index))
current_node = self.get_node(index)
left_child_idx = current_node.get_idx_left_child()
right_child_idx = current_node.get_idx_right_child()
if left_child_idx in self.tree_structure or right_child_idx in self.tree_structure:
raise TreeStructureError('Invalid removal of node, leaving two orphans nodes')
del self.tree_structure[index]
self.num_nodes -= 1
if index in self.idx_leaf_nodes:
self.idx_leaf_nodes.remove(index)Tree nodes
Both splitting and leaf nodes inherit from a base class called BaseNode which has two attributes: index and depth.
class BaseNode:
def __init__(self, index):
self.index = index
self.depth = int(math.floor(math.log(index+1, 2)))The splitting nodes should maintain the splitting variable and the value to split. Since BART allows for quantitative and qualitative splitting nodes we should make that distinction possible.
class SplitNode(BaseNode):
def __init__(self, index, idx_split_variable, type_split_variable, split_value):
super().__init__(index)
self.idx_split_variable = idx_split_variable
self.type_split_variable = type_split_variable
self.split_value = split_value
self.operator = '<=' if self.type_split_variable == 'quantitative' else 'in'The leaf nodes only hold the response result of the tree for a particular predictor space.
class LeafNode(BaseNode):
def __init__(self, index, value):
super().__init__(index)
self.value = valueFunctions to grow and prune the tree
Every tree can only grow from a leaf node. When this happen, the old node is replaced for a splitting node and two leaf nodes. On the other hand, when we prune a tree, we select a prunable node (splitting node that have two leaf nodes as children) from the tree, delete its children and replace the node for a leaf node.
class Tree:
def grow_tree(self, index_leaf_node, new_split_node, new_left_node, new_right_node):
current_node = self.get_node(index_leaf_node)
if not isinstance(current_node, LeafNode):
raise TreeStructureError('The tree grows from the leaves')
if not isinstance(new_split_node, SplitNode):
raise TreeStructureError('The node that replaces the leaf node must be SplitNode')
if not isinstance(new_left_node, LeafNode) or not isinstance(new_right_node, LeafNode):
raise TreeStructureError('The new leaves must be LeafNode')
self.delete_node(index_leaf_node)
self.set_node(index_leaf_node, new_split_node)
self.set_node(new_left_node.index, new_left_node)
self.set_node(new_right_node.index, new_right_node)
def prune_tree(self, index_split_node, new_leaf_node):
current_node = self.get_node(index_split_node)
if not isinstance(current_node, SplitNode):
raise TreeStructureError('Only SplitNodes are prunable')
left_child_idx = current_node.get_idx_left_child()
right_child_idx = current_node.get_idx_right_child()
self.delete_node(left_child_idx)
self.delete_node(right_child_idx)
self.delete_node(index_split_node)
self.set_node(index_split_node, new_leaf_node)Checks of correctness of the tree
Although the user will not be creating trees, but since we want our code to fail as soon as something bad happens (specially during develping), we added checks of correctness of the tree and raised exceptions if something was wrong. We also created tests to control that after each commit the implementation is still correct.
All the code for the implementation of BART can be viewed in this branch of PyMC.